Thời gian đọc ước tính: 12 phút
Những điểm chính
- Định nghĩa: Hàm FACT giúp tính giai thừa của một số dương, ký hiệu là $n!$ trong toán học.
- Cú pháp đơn giản: Chỉ cần sử dụng công thức
=FACT(number)để nhận kết quả ngay lập tức. - Xử lý dữ liệu: Hàm tự động cắt bỏ phần thập phân của số không nguyên và trả về lỗi #NUM! nếu số là âm.
- Ứng dụng thực tế: Hỗ trợ tính toán xác suất, chỉnh hợp (Permutation), tổ hợp (Combination) và các bài toán thống kê trong kinh doanh.
- Giải pháp thay thế: Sử dụng hàm FACTDOUBLE cho giai thừa kép hoặc kết hợp hàm PRODUCT và SEQUENCE trong Excel hiện đại.
Trong quá trình phân tích dữ liệu và thống kê, giai thừa (Factorial) là một khái niệm toán học nền tảng, đặc biệt quan trọng trong lĩnh vực xác suất. Dù bạn là một chuyên gia phân tích tài chính hay một nhân viên quản lý kho hàng cần tính toán các phương án sắp xếp, việc tính giai thừa thủ công với các con số lớn là điều bất khả thi.
Excel cung cấp một giải pháp mạnh mẽ và chính xác thông qua hàm FACT. Bài viết này sẽ hướng dẫn bạn cách sử dụng hàm này từ cơ bản đến nâng cao, đồng thời giải thích các ứng dụng thực tế trong môi trường doanh nghiệp.
Tổng quan về Giai thừa (Factorial) trong Toán học
Trước khi áp dụng công thức trên máy tính, chúng ta cần hiểu rõ bản chất của giai thừa. Trong toán học, giai thừa của một số nguyên dương $n$, ký hiệu là $n!$, là tích của tất cả các số nguyên dương từ 1 đến $n$.
Công thức tổng quát được biểu diễn như sau:
$$n! = n times (n-1) times (n-2) times dots times 1$$
Ví dụ cụ thể:
Để tính giai thừa của 5 ($5!$), bạn thực hiện phép nhân:
$$5! = 5 times 4 times 3 times 2 times 1 = 120$$
Giai thừa tăng trưởng cực kỳ nhanh khi giá trị $n$ tăng lên. Ví dụ:
- $3! = 6$
- $6! = 720$
- $10! = 3.628.800$
Chính vì sự tăng trưởng theo cấp số nhân này, việc sử dụng Excel để tính toán là phương pháp tối ưu nhất để đảm bảo độ chính xác và tiết kiệm thời gian.
Hướng dẫn sử dụng hàm FACT trong Excel
Hàm FACT là hàm tích hợp sẵn (built-in function) trong Excel, thuộc nhóm hàm Toán học và Lượng giác (Math & Trig). Mục đích duy nhất của nó là trả về giai thừa của một số.
Cú pháp hàm
Cấu trúc của hàm rất đơn giản:
=FACT(number)Trong đó:
- number: Là giá trị không âm mà bạn muốn tính giai thừa. Đây có thể là một số cụ thể nhập trực tiếp, một tham chiếu đến ô chứa số, hoặc kết quả của một công thức khác.
Ví dụ minh họa cơ bản
Giả sử bạn cần tính giai thừa của số 5. Bạn có thể nhập công thức sau vào bất kỳ ô nào trong bảng tính:
=FACT(5)Excel sẽ trả về kết quả là 120.
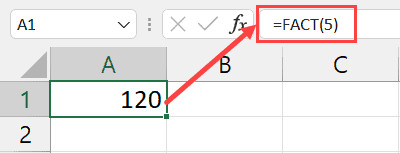FACT function in Excel to calculate factorial*Mô tả: Hình ảnh minh họa cách nhập hàm FACT(5) trong Excel để nhận kết quả là 120.*
Nếu giá trị số nằm ở ô A2, bạn sử dụng công thức:
=FACT(A2)Các quy tắc xử lý dữ liệu đặc biệt của hàm FACT
Mặc dù cú pháp đơn giản, hàm FACT có những quy tắc xử lý dữ liệu nghiêm ngặt mà người dùng cần nắm vững để tránh sai sót trong báo cáo.
1. Xử lý số thập phân (Decimal Numbers)
Hàm FACT được thiết kế để làm việc với số nguyên. Tuy nhiên, nếu bạn cung cấp một số thập phân, Excel sẽ không làm tròn (round) số đó mà sẽ cắt bỏ (truncate) phần thập phân để lấy phần nguyên trước khi tính toán.
Ví dụ:
- Công thức:
=FACT(5.9) - Excel xử lý: Hệ thống hiểu là
=FACT(5) - Kết quả: 120
Điều này khác hoàn toàn với việc làm tròn số học (nơi 5.9 sẽ được làm tròn thành 6). Người dùng cần lưu ý đặc điểm này khi làm việc với dữ liệu đo lường thực tế có chứa phần lẻ.
2. Xử lý số âm (Negative Numbers)
Giai thừa không được định nghĩa cho các số âm trong toán học cơ bản. Do đó, nếu tham số number là một số âm, Excel sẽ trả về thông báo lỗi.
Ví dụ:
- Công thức:
=FACT(-5) - Kết quả: #NUM!
Để khắc phục, bạn có thể kết hợp với hàm ABS để lấy giá trị tuyệt đối nếu dữ liệu đầu vào có thể bị âm do sai số nhập liệu: =FACT(ABS(-5)).
3. Trường hợp đặc biệt: Số 0
Theo quy ước toán học quốc tế, giai thừa của 0 ($0!$) luôn bằng 1. Excel tuân thủ chính xác quy tắc này.
Ví dụ:
- Công thức:
=FACT(0) - Kết quả: 1
Lý do $0! = 1$ liên quan đến khái niệm “tích rỗng” (empty product) và để đảm bảo tính nhất quán trong các công thức tổ hợp. Ví dụ, số cách chọn 0 phần tử từ một tập hợp $n$ phần tử là 1 (chính là tập rỗng).
Ứng dụng thực tế: Tính toán Xác suất và Thống kê
Sức mạnh thực sự của hàm FACT không nằm ở việc tính toán đơn lẻ, mà là khi nó trở thành một thành phần trong các công thức phức tạp hơn về xác suất, chỉnh hợp và tổ hợp. Dưới đây là các ví dụ ứng dụng trong môi trường doanh nghiệp và phân tích.
Bài toán Chỉnh hợp (Permutations)
Chỉnh hợp dùng để tính số cách sắp xếp một tập hợp các đối tượng theo một thứ tự nhất định.
Tình huống:
Bạn có 5 quả bóng màu khác nhau (Đỏ, Xanh, Vàng, Tím, Cam). Bạn muốn biết có bao nhiêu cách để chọn ra 2 quả bóng và sắp xếp chúng theo thứ tự (ví dụ: Đỏ – Xanh khác với Xanh – Đỏ).
Công thức toán học cho chỉnh hợp chập $k$ của $n$ phần tử ($P(n, k)$) là:
$$P(n, k) = frac{n!}{(n-k)!}$$
Áp dụng trong Excel:
Với $n=5$ và $k=2$, bạn có thể dùng công thức kết hợp hàm FACT:
=FACT(5) / FACT(5-2)Hoặc:
=FACT(5) / FACT(3)Kết quả sẽ là 20 cặp màu khác nhau.
Lưu ý: Excel có hàm chuyên dụng =PERMUT(5, 2) để tính chỉnh hợp, nhưng việc hiểu cách dùng FACT giúp bạn kiểm soát các biến thể của công thức khi cần tùy chỉnh.
Bài toán Tổ hợp (Combinations)
Tổ hợp dùng để tính số cách chọn các đối tượng mà không quan tâm đến thứ tự sắp xếp.
Tình huống:
Trong một đội nhóm gồm 10 nhân viên, bạn cần chọn ra 3 người để tham gia một dự án đặc biệt. Thứ tự chọn không quan trọng, miễn là 3 người đó có trong danh sách.
Công thức toán học cho tổ hợp ($C(n, k)$):
$$C(n, k) = frac{n!}{k!(n-k)!}$$
Áp dụng trong Excel:
Với $n=10$ và $k=3$:
=FACT(10) / (FACT(3) * FACT(10-3))Kết quả là 120 cách chọn nhóm khác nhau. Tương tự, bạn có thể dùng hàm =COMBIN(10, 3) để tính nhanh hơn, nhưng công thức FACT minh họa rõ bản chất toán học phía sau.
Phân phối Poisson trong Quản lý Kho (Inventory Management)
Trong quản trị chuỗi cung ứng, phân phối Poisson được dùng để dự báo số lượng sự kiện xảy ra trong một khoảng thời gian cố định (ví dụ: số lượng khách hàng đến cửa hàng trong 1 giờ).
Công thức Poisson:
$$P(x; lambda) = frac{e^{-lambda} cdot lambda^x}{x!}$$
Trong đó $x!$ (giai thừa của số sự kiện) là mẫu số quan trọng. Việc sử dụng hàm FACT ở đây giúp các nhà quản lý tính toán xác suất hết hàng hoặc dư thừa tồn kho một cách chính xác.
Các biến thể và Hàm liên quan
Bên cạnh hàm FACT cơ bản, Excel cung cấp các công cụ mở rộng để xử lý các nhu cầu tính toán nâng cao hơn.
Hàm FACTDOUBLE (Giai thừa kép)
Giai thừa kép (ký hiệu $n!!$) khác với giai thừa thường. Nó là tích của các số nguyên cùng tính chất chẵn/lẻ với $n$ và nhỏ hơn hoặc bằng $n$.
- Nếu $n$ chẵn: $n!! = n times (n-2) times (n-4) times dots times 2$
- Nếu $n$ lẻ: $n!! = n times (n-2) times (n-4) times dots times 1$
Cú pháp:
=FACTDOUBLE(number)Ví dụ:
=FACTDOUBLE(6)sẽ tính $6 times 4 times 2 = 48$.=FACTDOUBLE(5)sẽ tính $5 times 3 times 1 = 15$.
Hàm GAMMA (Dành cho số không nguyên)
Nếu bạn cần tính “giai thừa” cho các số không nguyên (ví dụ 5.5), hàm FACT không thể đáp ứng vì nó sẽ cắt bỏ phần thập phân. Trong toán học cao cấp, hàm Gamma ($Gamma$) là phần mở rộng của giai thừa cho số thực và số phức.
Mối quan hệ là: $Gamma(n) = (n-1)!$
Do đó, để tính giai thừa cho số thực $n$, bạn có thể dùng công thức:
=GAMMA(n+1)Ví dụ, để tính giá trị tương đương giai thừa của 5.5:
=GAMMA(5.5 + 1)Kết quả sẽ là 287.88, một con số chính xác mà hàm FACT không thể cung cấp.
Giải pháp thay thế hàm FACT trong Excel hiện đại
Nếu bạn đang sử dụng phiên bản Excel 365 hoặc Excel 2021 trở lên, bạn có thể tận dụng các hàm mảng động (Dynamic Arrays) để tạo ra công thức tính giai thừa tùy biến mà không cần dùng hàm FACT. Điều này hữu ích khi bạn muốn hiểu sâu về cách dữ liệu được xử lý hoặc cần tạo ra một chuỗi giai thừa.
Sử dụng kết hợp hàm SEQUENCE và PRODUCT:
Công thức:
=PRODUCT(SEQUENCE(n))Giải thích:
- SEQUENCE(n): Tạo ra một mảng các số từ 1 đến $n$. Ví dụ
SEQUENCE(5)tạo ra mảng{1; 2; 3; 4; 5}. - PRODUCT(…): Nhân tất cả các số trong mảng đó lại với nhau. $1 times 2 times 3 times 4 times 5 = 120$.
Phương pháp này cho kết quả tương đương với =FACT(5) nhưng linh hoạt hơn trong các mô hình tài chính phức tạp cần thao tác trên từng phần tử của mảng số.
Bảng tổng hợp các lỗi thường gặp
Khi làm việc với hàm FACT, bạn có thể gặp một số mã lỗi. Dưới đây là bảng tra cứu nhanh nguyên nhân và cách khắc phục:
| Mã Lỗi | Nguyên Nhân | Giải Pháp Khắc Phục |
|---|---|---|
| #NUM! | Tham số nhập vào là số âm (ví dụ: -1, -10). | Kiểm tra lại dữ liệu đầu vào. Sử dụng hàm ABS() nếu cần lấy giá trị tuyệt đối. |
| #NUM! | Kết quả quá lớn vượt quá khả năng hiển thị của Excel. | Excel chỉ hỗ trợ hiển thị số đến $1.79 times 10^{308}$. Giai thừa của 171 trở lên sẽ gây lỗi này. |
| #VALUE! | Tham số không phải là số (ví dụ: văn bản “abc”). | Đảm bảo ô tham chiếu chứa dữ liệu dạng số (Number). |
| #NAME? | Sai tên hàm (ví dụ: =FACTT(5)). | Kiểm tra lại chính tả tên hàm là FACT. |
Câu hỏi thường gặp (FAQ)
Hàm FACT có tính được giai thừa của số lớn như 200 không?
Không. Excel có giới hạn về độ lớn của số mà nó có thể xử lý. Giai thừa của 170 là con số lớn nhất mà Excel có thể tính toán và hiển thị ($170! approx 7.26 times 10^{306}$). Nếu bạn tính =FACT(171), Excel sẽ trả về lỗi #NUM! do hiện tượng tràn số (overflow).
Làm thế nào để tính giai thừa của một cột số liệu?
Bạn chỉ cần nhập công thức =FACT(A1) vào ô đầu tiên của cột kết quả (ví dụ B1), sau đó nhấn đúp vào Fill Handle (góc dưới bên phải ô B1) để sao chép công thức xuống toàn bộ cột. Excel sẽ tự động tính giai thừa cho từng hàng tương ứng.
Có sự khác biệt nào giữa FACT và COMBIN không?
Có. FACT tính giai thừa của một số duy nhất ($n!$). COMBIN tính số tổ hợp chập $k$ của $n$, sử dụng giai thừa làm một phần của công thức tính toán. COMBIN(n, k) thực chất là kết quả của phép tính FACT(n) / (FACT(k) * FACT(n-k)).
Tại sao FACT(5.9) lại bằng 120 mà không phải số lớn hơn?
Vì hàm FACT chỉ nhận phần nguyên của tham số. Nó coi 5.9 là 5. Nếu bạn muốn tính giai thừa chính xác cho số thực (Interpolated Factorial), bạn phải sử dụng hàm GAMMA(5.9 + 1).
Hàm FACT có hoạt động trên Google Sheets không?
Có. Hàm FACT trên Google Sheets hoạt động hoàn toàn giống với Excel, bao gồm cả cú pháp và cách xử lý số âm hay số thập phân. Bạn có thể áp dụng kiến thức trong bài viết này cho cả hai nền tảng.
Nguồn tham khảo
Để tìm hiểu sâu hơn về các hàm toán học và ứng dụng thống kê, bạn có thể tham khảo các nguồn uy tín sau:
- Microsoft Support: Hàm FACT – Hỗ trợ của Microsoft
- Wolfram MathWorld: Factorial Definition & Properties
- Investopedia: Permutations and Combinations in Finance
- Khan Academy: Giới thiệu về Giai thừa và Tổ hợp
