Hướng Dẫn Tính NPV Trong Excel: Công Thức, Ví Dụ Và Cách Dùng Hàm XNPV

Thời gian đọc ước tính: 12 phút

Những điểm chính

• Hiểu bản chất NPV: Net Present Value (Giá trị hiện tại ròng) là công cụ cốt lõi để đánh giá khả năng sinh lời của dự án dựa trên giá trị thời gian của tiền.
• Hàm NPV cơ bản: Cách sử dụng hàm =NPV() cho các dòng tiền đều đặn xảy ra vào cuối kỳ.
• Xử lý dòng tiền đầu kỳ: Kỹ thuật điều chỉnh công thức khi khoản đầu tư ban đầu xảy ra ngay tại thời điểm hiện tại (năm 0).
• Hàm XNPV nâng cao: Giải pháp tính toán chính xác cho các dòng tiền không đều hoặc diễn ra vào các ngày cụ thể.
• So sánh dự án: Phương pháp dùng NPV để lựa chọn phương án đầu tư tối ưu nhất giữa nhiều lựa chọn.

Net Present Value (NPV) hay Giá trị hiện tại ròng, là một trong những phương pháp phân tích tài chính quan trọng nhất để xác định xem một dự án hoặc khoản đầu tư có mang lại lợi nhuận thực tế hay không. Trong thế giới tài chính doanh nghiệp và đầu tư cá nhân, NPV được xem là “thước đo vàng” giúp các nhà quản lý đưa ra quyết định chính xác dựa trên dữ liệu thay vì cảm tính.

Hãy hình dung bạn có một kế hoạch đầu tư: Bạn bỏ ra 100 USD mỗi tháng trong 10 năm tới và nhận lại 20.000 USD khi kết thúc chu kỳ. Làm thế nào để biết con số 20.000 USD đó trong tương lai có giá trị hơn hay kém hơn tổng số tiền bạn bỏ ra, khi tính đến lạm phát và cơ hội đầu tư khác? NPV chính là công cụ giải quyết bài toán này.

Trong bài viết chuyên sâu này, chúng ta sẽ đi qua các ví dụ thực tế về cách tính toán NPV trong Microsoft Excel. Edupedia sẽ hướng dẫn bạn sử dụng hai công thức cốt lõi: Hàm NPV (cho dòng tiền đều) và Hàm XNPV (cho dòng tiền theo ngày cụ thể).

NPV Là Gì? Giải Thích Đơn Giản Về Giá trị Hiện Tại Ròng

Trước khi đi vào các thao tác kỹ thuật trên Excel, chúng ta cần nắm vững bản chất của chỉ số này. NPV là tổng giá trị hiện tại của tất cả các dòng tiền trong tương lai (bao gồm cả dòng tiền dương và âm) được chiết khấu về thời điểm hiện tại.

Nguyên lý cơ bản nằm ở khái niệm “Giá trị thời gian của tiền” (Time Value of Money). Một khoản tiền 10.000 USD bạn nhận được hôm nay luôn có giá trị cao hơn 10.000 USD bạn nhận được sau 5 năm nữa. Lý do là vì tiền ở hiện tại có thể được mang đi đầu tư để sinh lời.

Ví dụ, giả sử có một cơ hội đầu tư yêu cầu bạn chi 10.000 USD ngay bây giờ (dòng tiền ra) và bạn sẽ nhận được 1.000 USD mỗi năm trong 20 năm tới (dòng tiền vào).

Để đánh giá, bạn cần một tỷ suất chiết khấu (discount rate) – thường là chi phí vốn hoặc lãi suất kỳ vọng. Bạn sử dụng tỷ lệ này trong công thức Excel để quy đổi toàn bộ 20.000 USD nhận được trong tương lai về giá trị của ngày hôm nay.

• Nếu NPV > 0: Giá trị thu về lớn hơn chi phí bỏ ra. Dự án có lãi, bạn nên đầu tư.
• Nếu NPV < 0: Giá trị thu về thấp hơn chi phí bỏ ra. Dự án thua lỗ, bạn nên từ chối và tìm kênh đầu tư khác an toàn hơn như trái phiếu chính phủ hoặc gửi tiết kiệm.

NPV đặc biệt hữu ích khi bạn cần đặt nhiều dự án lên bàn cân. Nếu có 3 dự án khả thi, dự án nào có NPV dương cao nhất sẽ là lựa chọn tối ưu về mặt tài chính.

Cấu Trúc Hàm NPV Trong Excel

Microsoft Excel cung cấp hàm có sẵn để tính toán nhanh chóng chỉ số này với cú pháp như sau:

=NPV(rate, value1, [value2],...)

Dưới đây là giải thích chi tiết các tham số trong công thức:

• rate (Tỷ suất): Đây là tỷ suất chiết khấu cho một kỳ. Nếu dòng tiền của bạn tính theo năm, đây là lãi suất năm. Nếu dòng tiền tính theo quý, bạn phải dùng lãi suất quý.
• value1, value2… (Giá trị): Đây là các dòng tiền phát sinh. Số dương đại diện cho thu nhập (inflow), số âm đại diện cho chi phí hoặc khoản thanh toán (outflow). Hàm hỗ trợ tối đa 254 giá trị.

Những lưu ý kỹ thuật bắt buộc:

1. Khoảng cách thời gian: Hàm NPV mặc định hiểu rằng các khoản tiền này xảy ra đều đặn theo thời gian (ví dụ: cuối mỗi năm hoặc cuối mỗi tháng). Khoảng cách giữa các kỳ phải bằng nhau.
2. Thứ tự nhập liệu: Thứ tự của các giá trị value trong công thức đại diện cho trình tự thời gian. Nếu bạn đảo lộn thứ tự, kết quả NPV sẽ sai lệch hoàn toàn.
3. Thời điểm dòng tiền: Công thức này giả định dòng tiền xảy ra vào cuối kỳ. Điều này rất quan trọng khi xử lý khoản đầu tư ban đầu (thường xảy ra ở đầu kỳ 1 hay còn gọi là năm 0).
4. Dữ liệu rỗng: Excel sẽ bỏ qua các ô trống hoặc chứa văn bản (text), chỉ tính toán trên các ô chứa số.

Nếu dữ liệu của bạn có dòng tiền phát sinh vào các ngày ngẫu nhiên không đều nhau, hàm NPV cơ bản sẽ không hoạt động chính xác. Khi đó, bạn buộc phải sử dụng hàm XNPV (sẽ được đề cập chi tiết ở phần sau).

Hướng Dẫn Tính NPV Trong Excel Qua Ví Dụ Thực Tế

Khi làm việc với các dự án tài chính, chúng ta thường gặp hai kịch bản dòng tiền chính:

1. Dòng tiền đầu tiên (thu hoặc chi) xảy ra vào cuối kỳ thứ nhất.
2. Dòng tiền đầu tiên (thường là vốn đầu tư) xảy ra ngay tại đầu kỳ thứ nhất (tức thì).

Ví dụ: Bạn đang đánh giá một dự án mở quán cà phê với vốn đầu tư ban đầu là 100.000 USD.

• Trường hợp 1: Bạn ký hợp đồng và thanh toán 100.000 USD vào cuối năm tài chính đầu tiên.
• Trường hợp 2: Bạn thanh toán 100.000 USD ngay lập tức khi bắt đầu dự án (đây là trường hợp phổ biến hơn trong thực tế).

Chúng ta sẽ xử lý từng trường hợp một cách chi tiết.

Trường hợp 1: Dòng tiền đầu tiên xảy ra vào cuối kỳ

Giả sử chúng ta có một bảng dữ liệu dự án với các dòng tiền như hình dưới đây và tỷ suất chiết khấu (discount rate) được xác định là 5%:

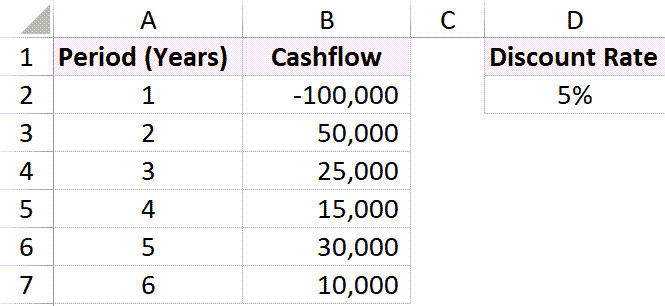Bảng dữ liệu tính toán NPV với dòng tiền bắt đầu từ cuối năm 1

Trong ví dụ này, khoản chi 100.000 USD (số âm) nằm ở dòng “Year 1”, tức là nó phát sinh vào cuối năm thứ nhất. Các dòng tiền thu về (số dương) phát sinh từ cuối năm 2 đến cuối năm 6.

Để tính NPV, bạn nhập công thức sau vào ô kết quả:

=NPV(D2, B2:B7)

Trong đó:

• D2: Là ô chứa tỷ suất chiết khấu (5%).
• B2:B7: Là dải ô chứa toàn bộ dòng tiền từ năm 1 đến năm 6.

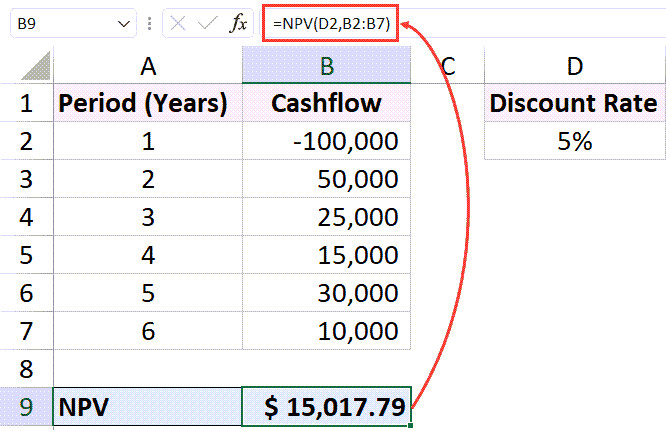Công thức Excel để tính NPV cho trường hợp dòng tiền cuối kỳ

Kết quả trả về là $15,017.

Điều này có nghĩa là: Với chi phí vốn 5%, dự án này không những hoàn vốn mà còn tạo ra thêm một giá trị hiện tại ròng là 15,017 USD. Đây là một dự án “xanh”, đáng để đầu tư.

Trường hợp 2: Dòng tiền đầu tiên xảy ra vào đầu kỳ (Năm 0)

Đây là kịch bản sát với thực tế kinh doanh nhất: Bạn phải bỏ vốn ngay lập tức (Năm 0) trước khi vận hành. Tuy nhiên, hàm NPV của Excel mặc định tính dòng tiền đầu tiên là ở cuối kỳ 1. Nếu bạn đưa khoản đầu tư ban đầu vào thẳng trong hàm NPV, Excel sẽ hiểu sai rằng khoản tiền đó bị chiết khấu 1 năm, dẫn đến kết quả sai.

Dưới đây là dữ liệu cho trường hợp vốn đầu tư bỏ ra ngay ban đầu:

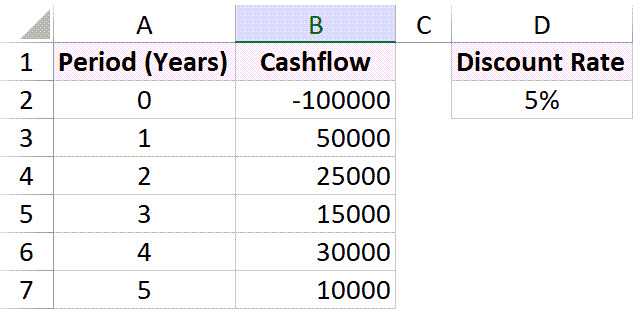Dữ liệu dòng tiền khi vốn đầu tư phát sinh ngay đầu kỳ

Để tính toán chính xác, chúng ta phải tách khoản đầu tư ban đầu ra khỏi hàm NPV. Công thức chuẩn sẽ là:

=B2 + NPV(D2, B3:B7)

Phân tích công thức:

• B2: Khoảng đầu tư ban đầu (-100.000 USD). Vì nó xảy ra ở hiện tại (Năm 0), giá trị của nó không bị chiết khấu, nên ta cộng trực tiếp vào kết quả.
• NPV(D2, B3:B7): Hàm NPV chỉ tính cho các dòng tiền từ năm 1 đến năm 5 (các dòng tiền tương lai cần chiết khấu).

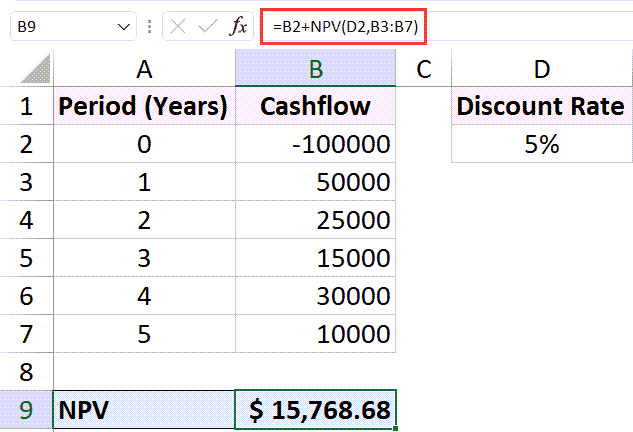Công thức điều chỉnh để tính NPV khi có vốn đầu tư ban đầu

Kết quả trả về là $15,768.

Bạn có thể thấy, cùng một bộ số liệu dòng tiền, nhưng việc bỏ vốn sớm hơn (đầu kỳ so với cuối kỳ 1) và thu tiền sớm hơn đã làm thay đổi giá trị NPV. Việc hiểu rõ thời điểm dòng tiền là yếu tố sống còn để tính toán chính xác.

Tìm hiểu thêm: Để hiểu rõ hơn về cách tính trung bình trong các báo cáo tài chính, bạn có thể tham khảo bài viết về Công thức tính trung bình gia quyền trong Excel.

So Sánh Các Dự Án Đầu Tư Bằng NPV

Trong quản trị doanh nghiệp, nguồn vốn là hữu hạn. Bạn thường xuyên phải đối mặt với việc lựa chọn giữa Dự án A, Dự án B hay Dự án C. NPV là công cụ khách quan nhất để so sánh vì nó quy đổi mọi thứ về cùng một mặt bằng giá trị hiện tại.

Giả sử bạn là Giám đốc tài chính và cần chọn 1 trong 3 dự án dưới đây. Vốn đầu tư ban đầu đều là 100.000 USD, tỷ suất chiết khấu chung là 5%.

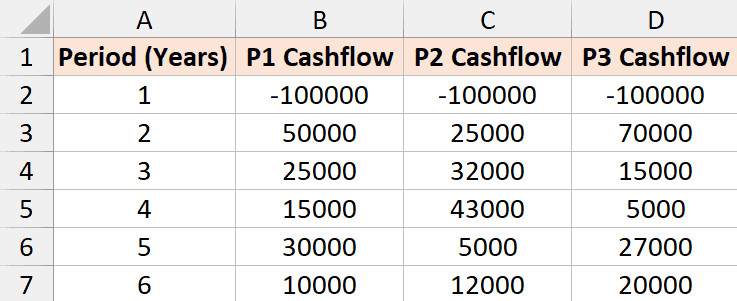Bảng dữ liệu so sánh 3 dự án đầu tư khác nhau

Chúng ta áp dụng công thức NPV cho từng cột dữ liệu (giả định dòng tiền đầu tiên xảy ra cuối năm 1 để đơn giản hóa việc so sánh công thức):

• Dự án 1: =NPV(5%, B2:B7)
• Dự án 2: =NPV(5%, C2:C7)
• Dự án 3: =NPV(5%, D2:D7)

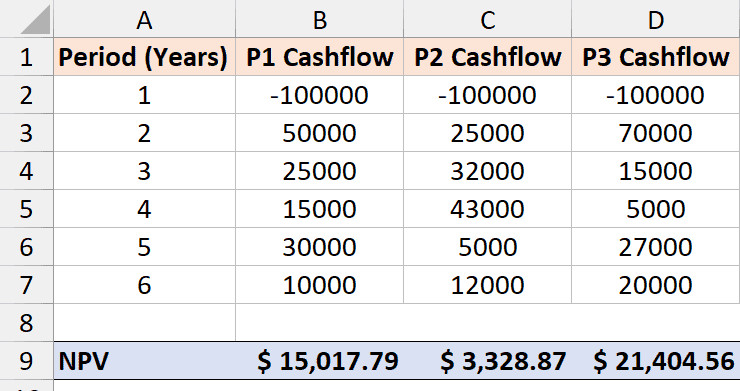Kết quả NPV của 3 dự án cho thấy sự chênh lệch lợi nhuận

Phân tích kết quả:

• Dự án 1: NPV = $15,017
• Dự án 2: NPV = $12,982
• Dự án 3: NPV = $19,252

Rõ ràng, Dự án 3 mang lại giá trị hiện tại ròng cao nhất. Nếu chỉ được chọn một, Dự án 3 là ưu tiên hàng đầu. Nếu nguồn vốn cho phép chọn hai dự án, bạn nên kết hợp Dự án 3 và Dự án 1 để tối đa hóa lợi nhuận tổng thể.

Một điểm cần lưu ý: NPV dựa trên dự báo. Các dòng tiền ở năm thứ 1, thứ 2 có độ tin cậy cao, nhưng dòng tiền ở năm thứ 10 hoặc 20 chứa đựng rủi ro sai số rất lớn. Do đó, các nhà phân tích thường chạy thêm các kịch bản “độ nhạy” (Sensitivity Analysis) với các tỷ suất chiết khấu khác nhau để kiểm tra độ bền vững của dự án.

Tính NPV Cho Dòng Tiền Không Đều Với Hàm XNPV

Thực tế kinh doanh hiếm khi “đẹp” như lý thuyết sách vở. Khách hàng không trả tiền đúng ngày 31/12 hàng năm. Các khoản chi phát sinh vào ngày 15/3, doanh thu về vào ngày 20/8. Khi khoảng cách giữa các dòng tiền không đều nhau, hàm NPV thường sẽ cho kết quả sai lệch.

Excel cung cấp hàm XNPV để giải quyết triệt để vấn đề này. Hàm này yêu cầu bạn nhập chính xác ngày tháng tương ứng với từng dòng tiền.

Cú pháp hàm XNPV:
=XNPV(rate, values, dates)

Các tham số bao gồm:

• rate: Tỷ suất chiết khấu theo năm.
• values: Dãy giá trị dòng tiền (bao gồm cả thu và chi).
• dates: Dãy các ngày tháng tương ứng với dòng tiền.

Nguyên tắc quan trọng: Ngày đầu tiên trong dãy dates được xem là ngày bắt đầu. Tất cả các dòng tiền sau đó sẽ được chiết khấu dựa trên số ngày thực tế chênh lệch so với ngày đầu tiên này.

Ví dụ: Chúng ta có một dự án với các mốc thời gian giải ngân và thu tiền cụ thể như sau:

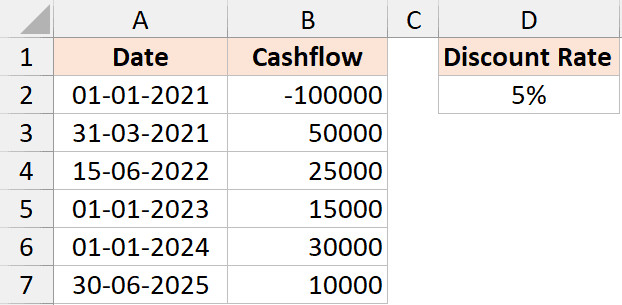Dữ liệu dòng tiền gắn liền với các ngày cụ thể

Công thức tính toán sẽ là:
=XNPV(D2, B2:B7, A2:A7)

Trong đó:

• D2: Tỷ suất 5%.
• B2:B7: Các giá trị tiền tệ.
• A2:A7: Các mốc thời gian tương ứng.

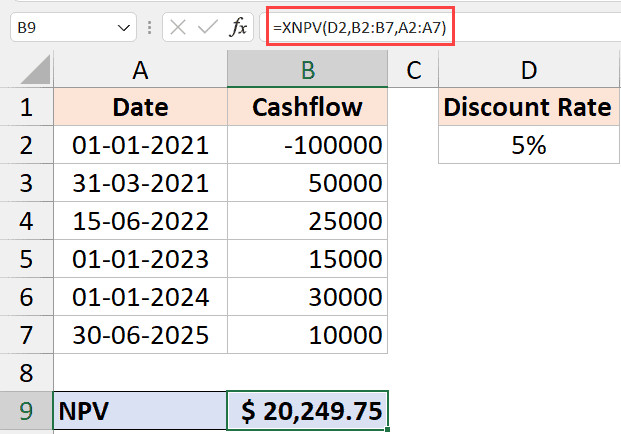Sử dụng hàm XNPV để tính toán chính xác theo ngày

Kết quả trả về sẽ phản ánh chính xác giá trị thời gian của từng đồng tiền dựa trên số ngày thực tế nó nằm trong dự án. Đối với các hợp đồng tài chính, bất động sản hay xây dựng kéo dài, XNPV là hàm bắt buộc phải dùng thay vì NPV thông thường.

Nên Dùng NPV Hay IRR?

Trong thẩm định đầu tư, bạn sẽ thường xuyên nghe đến IRR (Internal Rate of Return – Tỷ suất hoàn vốn nội bộ). Vậy đâu là chỉ số nên tin dùng?

• NPV (Giá trị hiện tại ròng): Cho biết giá trị tuyệt đối (số tiền cụ thể) mà dự án mang lại.
• IRR (Tỷ suất hoàn vốn nội bộ): Cho biết tỷ suất sinh lời phần trăm của dự án (mức lãi suất mà tại đó NPV = 0).

Mặc dù cả hai thường dẫn đến cùng một quyết định đầu tư, nhưng NPV được giới tài chính đánh giá cao hơn về độ tin cậy.

Lý do là IRR có một số hạn chế kỹ thuật (như trường hợp dòng tiền đổi dấu nhiều lần sẽ tạo ra nhiều giá trị IRR ảo). Ngoài ra, NPV cho bạn thấy quy mô thực của lợi nhuận. Một dự án có IRR 50% nhưng chỉ lãi 1.000 USD sẽ kém hấp dẫn hơn một dự án có IRR 20% nhưng mang lại 1 triệu USD lợi nhuận ròng.

Trong trường hợp kết quả giữa NPV và IRR mâu thuẫn nhau khi so sánh hai dự án độc lập, hãy ưu tiên quyết định theo NPV.

Câu hỏi thường gặp (FAQ)

1. Tỷ suất chiết khấu (Discount rate) trong công thức nên lấy bao nhiêu?
Tỷ suất này thường là Chi phí vốn bình quân gia quyền (WACC) của doanh nghiệp, hoặc lãi suất vay ngân hàng cộng với một biên độ rủi ro, hoặc mức lợi nhuận kỳ vọng tối thiểu mà nhà đầu tư mong muốn.

2. Nếu NPV bằng 0 thì có nên đầu tư không?
Về lý thuyết, NPV = 0 nghĩa là dự án vừa đủ hoàn vốn và đạt mức lợi nhuận kỳ vọng (đúng bằng tỷ suất chiết khấu). Bạn có thể đầu tư nếu mục tiêu là mở rộng thị phần hoặc duy trì hoạt động, nhưng nó không tạo ra giá trị thặng dư vượt trội.

3. Tại sao hàm NPV trong Excel lại tính sai dòng tiền năm 0?
Hàm NPV của Excel được lập trình dựa trên giả định kỳ đầu tiên là kỳ 1 (cuối năm 1). Do đó, nó sẽ chiết khấu giá trị đầu tiên trong dãy. Để sửa, bạn cần đưa dòng tiền năm 0 ra ngoài công thức cộng.

4. Hàm XNPV báo lỗi #NUM! hoặc #VALUE! là do đâu?
Lỗi này thường xảy ra nếu các ô ngày tháng (dates) không được định dạng đúng chuẩn Date của Excel (ví dụ đang ở dạng Text), hoặc độ dài của dãy values và dãy dates không bằng nhau.

5. Có thể dùng NPV để tính lỗ lãi chứng khoán không?
Có thể, nhưng NPV phù hợp hơn cho các dự án dài hạn với dòng tiền dự báo trước. Chứng khoán biến động quá nhanh theo phiên nên thường dùng các chỉ số khác như ROI hoặc P/E để đánh giá.

Nguồn tham khảo

Để đảm bảo tính chính xác và cập nhật kiến thức chuyên sâu, bài viết sử dụng thông tin từ các nguồn uy tín sau:

1. Microsoft Support: Hướng dẫn kỹ thuật chính thức về hàm NPV và XNPV từ nhà phát triển Excel.
   • URL: https://support.microsoft.com/vi-vn/office/hàm-npv-8672cb67-2576-4d07-b67b-ac28acf2a568
2. Investopedia: Bách khoa toàn thư về tài chính, cung cấp định nghĩa chuẩn về Net Present Value và so sánh với IRR.
   • URL: https://www.investopedia.com/terms/n/npv.asp
3. Corporate Finance Institute (CFI): Tài liệu đào tạo phân tích tài chính chuyên nghiệp về các phương pháp thẩm định vốn.
   • URL: https://corporatefinanceinstitute.com/resources/valuation/net-present-value-npv/

Thông qua bài viết này, hy vọng bạn đã nắm vững cách sử dụng các hàm tài chính mạnh mẽ trong Excel để đưa ra những quyết định đầu tư thông minh và chính xác hơn.